Data Science for Actuaries

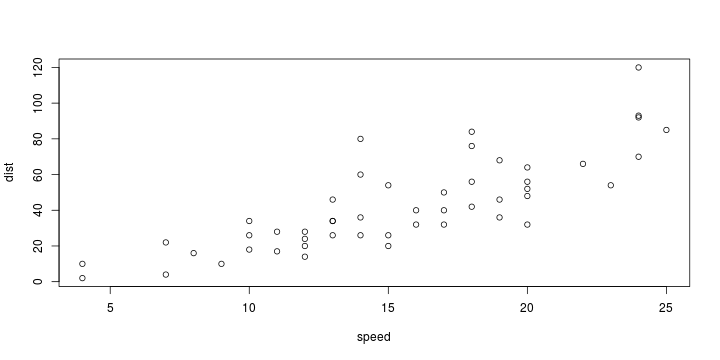
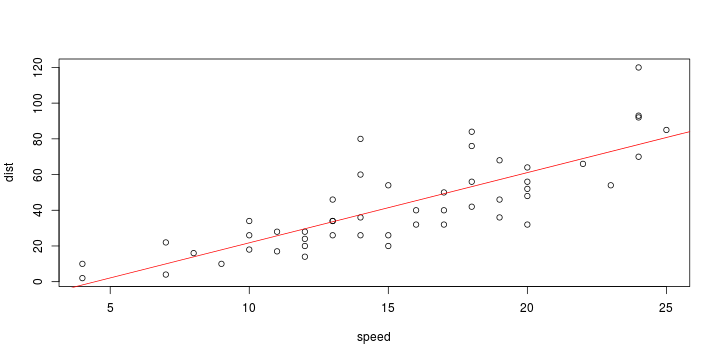
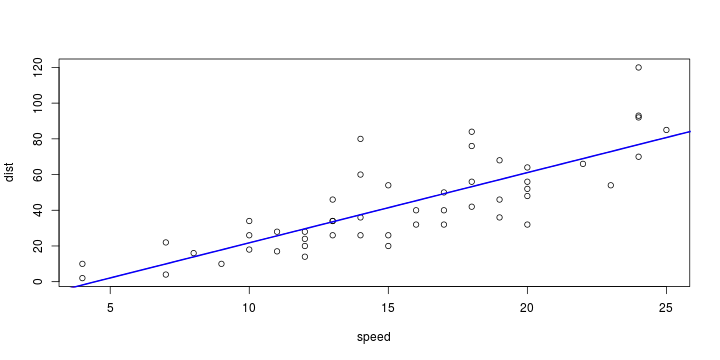
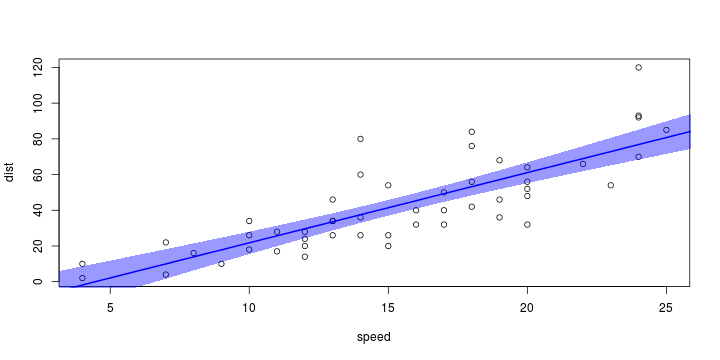
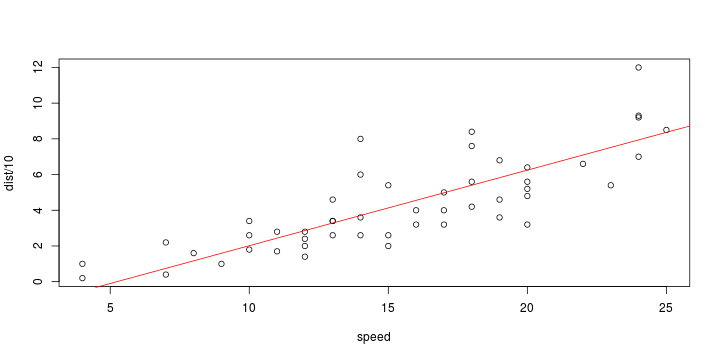
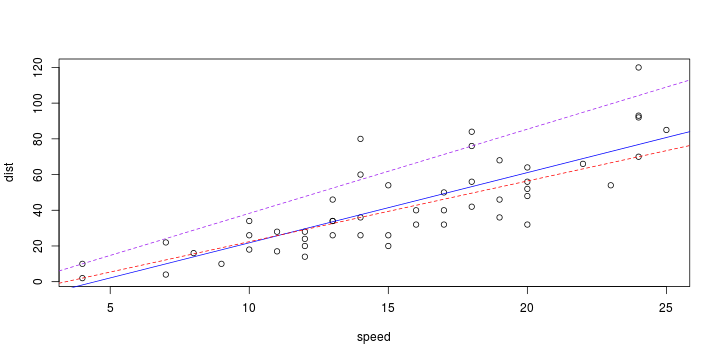
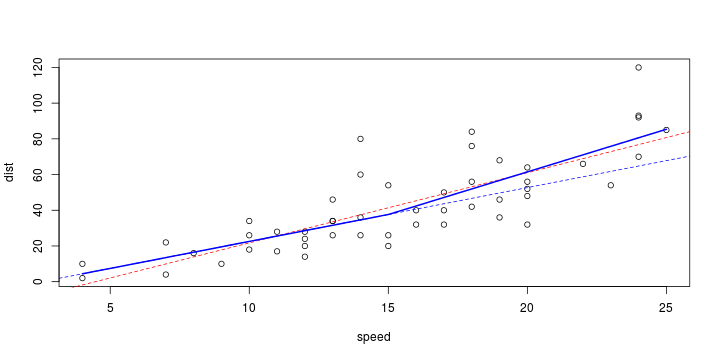
\[ y_i=\boldsymbol{x}_i^{\text{T}}\boldsymbol{\beta}+\varepsilon_i=\beta_0 + [\beta_1 x_{1,i}+\cdots+ \beta_k x_{k,i}]+\varepsilon_i \]

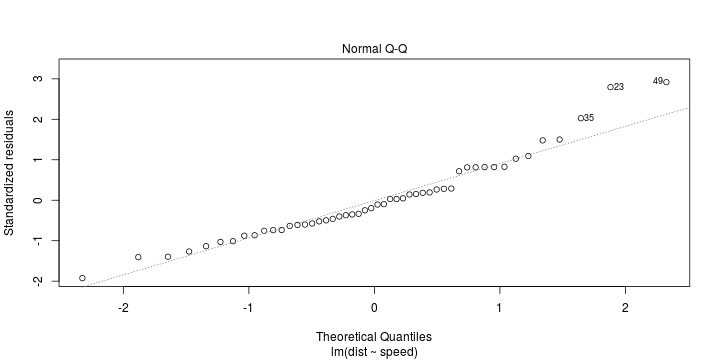
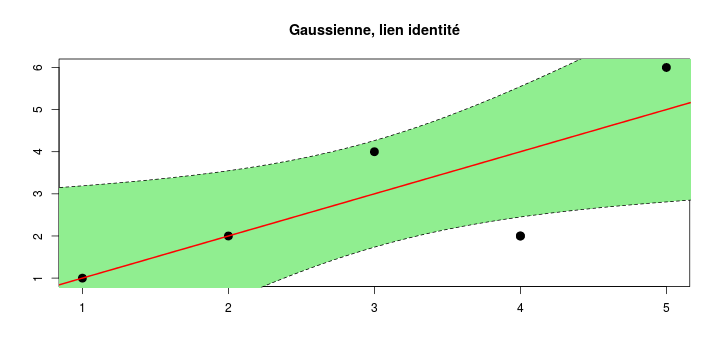
See linear model, where \(\varepsilon_i\sim\mathcal{N}(0,\sigma^2)\) i.id.

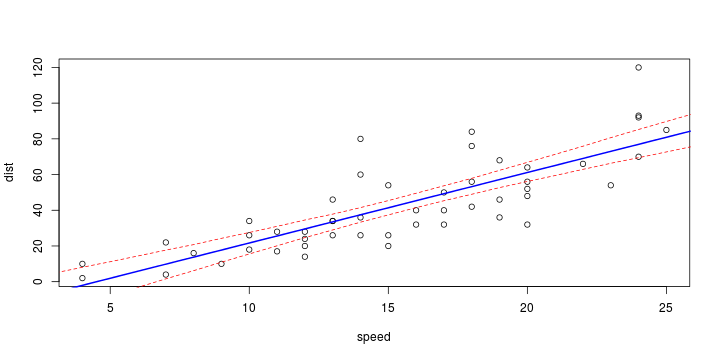
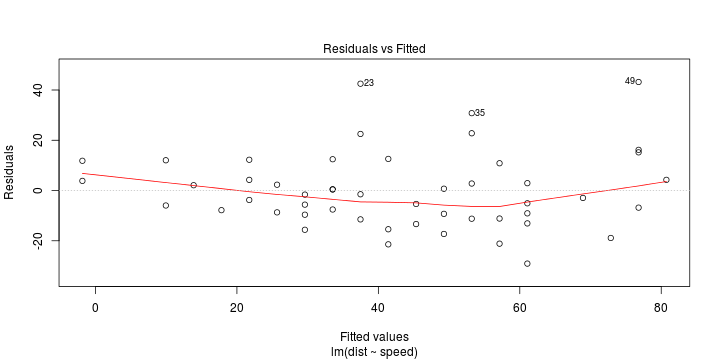
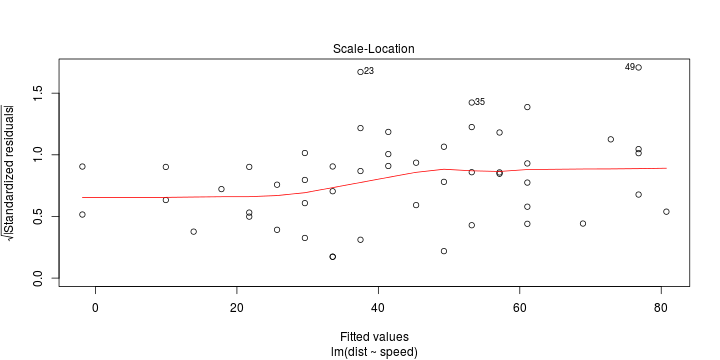
\[ (Y\vert \boldsymbol{X}=\boldsymbol{x})\sim \mathcal{N}(\boldsymbol{x}^{\text{T}}\boldsymbol{\beta}, \sigma^2) \] i.e. \[ \mathbb{E}[Y\vert\boldsymbol{X}=\boldsymbol{x}]=\boldsymbol{x}^{\text{T}}\boldsymbol{\beta} \] and homoscedastic model, \[ \text{Var}[Y\vert\boldsymbol{X}=\boldsymbol{x}]=\sigma^2 \]

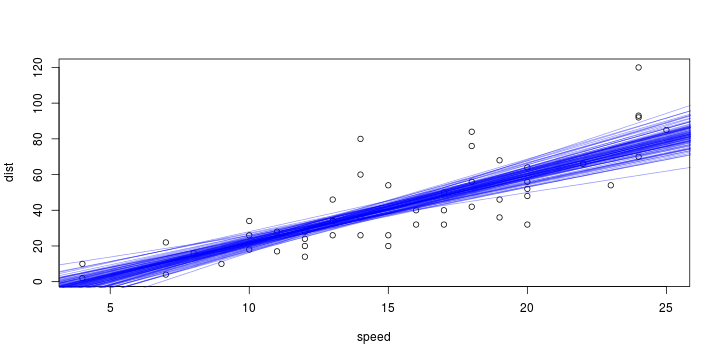
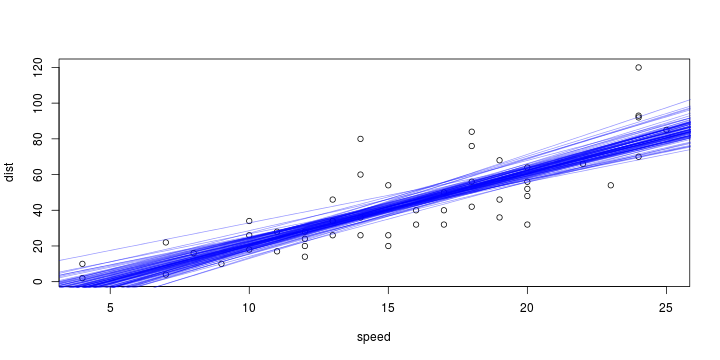
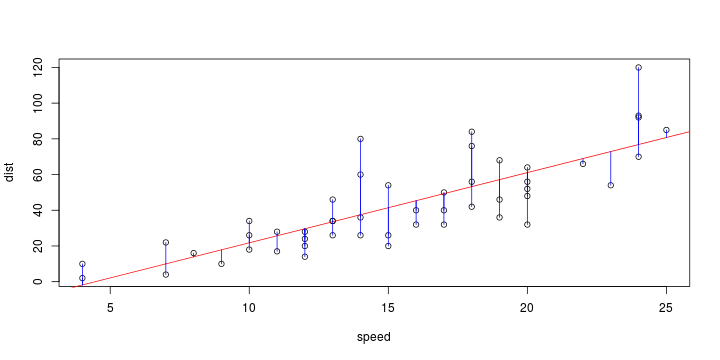
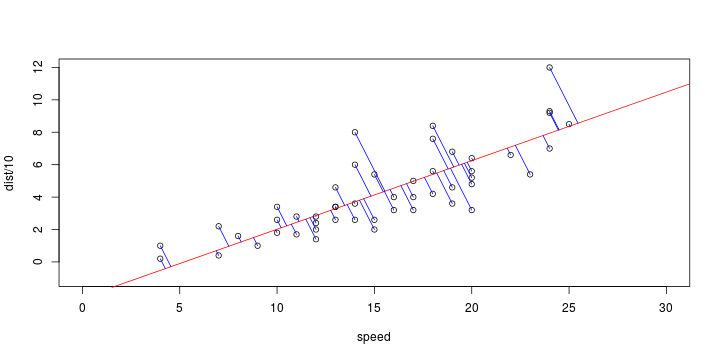
Least squares (and maximum likelihood) estimator \[ \widehat{\boldsymbol{\beta}}=\text{argmin} \left\lbrace \sum_{i=1}^n (y_i-\boldsymbol{x}_i^{\text{T}}\boldsymbol{\beta})^2 \right\rbrace =(\boldsymbol{X}^{\text{T}}\boldsymbol{X})^{-1}\boldsymbol{X}^{\text{T}}\boldsymbol{y}\]

plot(cars)

model <- lm(dist ~ speed, data=cars)

summary(model)

## 
## Call:
## lm(formula = dist ~ speed, data = cars)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -29.069  -9.525  -2.272   9.215  43.201 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -17.5791     6.7584  -2.601   0.0123 *  
## speed         3.9324     0.4155   9.464 1.49e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 15.38 on 48 degrees of freedom
## Multiple R-squared:  0.6511, Adjusted R-squared:  0.6438 
## F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12

X=cbind(1,cars$speed)
Y=cars$dist
solve(crossprod(X,X),crossprod(X,Y))

##            [,1]
## [1,] -17.579095
## [2,]   3.932409

model$coefficients

## (Intercept)       speed 
##  -17.579095    3.932409

summary(model)$sigma^2*solve(crossprod(X,X))

##           [,1]       [,2]
## [1,] 45.676514 -2.6588234
## [2,] -2.658823  0.1726509

vcov(model)

##             (Intercept)      speed
## (Intercept)   45.676514 -2.6588234
## speed         -2.658823  0.1726509

n=nrow(cars)

confint(model)

##                  2.5 %    97.5 %
## (Intercept) -31.167850 -3.990340
## speed         3.096964  4.767853

model$coefficients[1]+qt(c(.025,.975),n-2)* summary(model)$coefficients[1,2]

## [1] -31.16785  -3.99034

coefficient of determination \(\displaystyle{R^2 = \frac{\text{explained variance}}{\text{total variance}}}\)

summary(model)$r.squared

## [1] 0.6510794

1-deviance(model)/sum((Y-mean(Y))^2)

## [1] 0.6510794

\[ \text{Var}[Y]= \text{Var}[\mathbb{E}[Y\vert X]]+ \mathbb{E}[\text{Var}[Y\vert X]] \]

see analysis of variance

\[ \overline{R}^2 = 1-[1-R^2]\cdot \frac{n-1}{n-(k-1)-1} \]

summary(model)$adj.r.squared

## [1] 0.6438102

anova(lm(dist~speed,data=cars),lm(dist~1,data=cars))

## Analysis of Variance Table
## 
## Model 1: dist ~ speed
## Model 2: dist ~ 1
##   Res.Df   RSS Df Sum of Sq      F   Pr(>F)    
## 1     48 11354                                 
## 2     49 32539 -1    -21186 89.567 1.49e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

plot(cars)
abline(model,col="red")

plot(cars)
abline(model,col="red")
x=seq(2,26)
y=predict(model, newdata=data.frame(speed=x))
lines(x,y,lwd=2,col="blue")

y=predict(model, newdata=data.frame(speed=x), interval = "confidence")
head(y)

##         fit        lwr       upr
## 1 -9.714277 -21.733068  2.304513
## 2 -5.781869 -17.026591  5.462853
## 3 -1.849460 -12.329543  8.630624
## 4  2.082949  -7.644150 11.810048
## 5  6.015358  -2.973341 15.004056
## 6  9.947766   1.678977 18.216556

\[ \text{Var}[\widehat{Y}(\boldsymbol{x})]=\text{Var}[\boldsymbol{x}^{\text{T}}\widehat{\boldsymbol{\beta}}]=\boldsymbol{x}^{\text{T}}\text{Var}[\widehat{\boldsymbol{\beta}}]\boldsymbol{x} =\widehat{\sigma}^2 \boldsymbol{x}^{\text{T}}[\boldsymbol{X}^{\text{T}}\boldsymbol{X}]^{-1}\boldsymbol{x} \]

plot(cars)
polygon(c(x,rev(x)),c(y[,2],rev(y[,3])),col=rgb(0,0,1,.4),border=NA)
lines(x,y[,1],lwd=2,col="blue")

Method 1

Y=matrix(NA,1000,length(x))
for(b in 1:1000){
  idx <- sample(1:nrow(cars),size=nrow(cars),replace=TRUE)
  modelb <- lm(dist ~ speed, data=cars[idx,])
  Y[b,] <- predict(modelb, newdata=data.frame(speed=x))
}

See bootstrap, based on pseudo-sample \[ \lbrace(\boldsymbol{x}_{i_1},y_{i_1}), \cdots,(\boldsymbol{x}_{i_n},y_{i_n}) \rbrace \] where \((i_1,\cdots,i_n)\in\lbrace 1,2,\cdots,n\rbrace\).

Method 1

plot(cars)
for(b in 1:100) lines(x,Y[b,],col=rgb(0,0,1,.4))

plot(cars)
lines(x,apply(Y,2,mean),col="blue",lwd=2)
lines(x,apply(Y,2,function(x) quantile(x,.025)),col="red",lty=2)
lines(x,apply(Y,2,function(x) quantile(x,.975)),col="red",lty=2)

Method 2

pred_dist=predict(model)
epsilon  =residuals(model)
Y=matrix(NA,1000,length(x))
for(b in 1:1000){
  idx <- sample(1:nrow(cars),size=nrow(cars),replace=TRUE)
  carsb=data.frame(speed=cars$speed,
                   dist=pred_dist+epsilon[idx])
  modelb <- lm(dist ~ speed, data=carsb)
  Y[b,] <- predict(modelb, newdata=data.frame(speed=x))
}

See bootstrap, based on pseudo-sample \[ \lbrace(\boldsymbol{x}_{1},\widehat{y}_{1}+\widehat{\varepsilon}_{i_1}), \cdots,(\boldsymbol{x}_{n},\widehat{y}_{n}+\widehat{\varepsilon}_{i_n}) \rbrace \] where \((i_1,\cdots,i_n)\in\lbrace 1,2,\cdots,n\rbrace\).

Method 2

plot(cars)
for(b in 1:100) lines(x,Y[b,],col=rgb(0,0,1,.4))

plot(cars)
lines(x,apply(Y,2,mean),col="blue",lwd=2)
lines(x,apply(Y,2,function(x) quantile(x,.025)),col="red",lty=2)
lines(x,apply(Y,2,function(x) quantile(x,.975)),col="red",lty=2)

plot(cars)
abline(model,col="red")
segments(cars$speed,cars$dist,cars$speed,predict(model),col="blue")

cars2=cars; cars2[,2]=cars[,2]/10
plot(cars2,ylab="dist/10")
acp=princomp(cars2)
b=acp$loadings[2,1]/acp$loadings[1,1]
a=acp$center[2]-b*acp$center[1]
abline(a,b,col="red")

plot(cars2,ylab="dist/10",xlim=c(0,30),ylim=c(-1,12))
abline(a,b,col="red")
t <- acp$loadings[,1] %*% (t(cars2)-acp$center)
X1 <- acp$center[1] +t * acp$loadings[1,1]
X2 <- acp$center[2] +t * acp$loadings[2,1]
segments(cars2$speed,cars2$dist,X1,X2,col="blue")

  f <- function(a) sum(abs(cars$dist-(a[1]+a[2]*cars$speed))) 
  opt <- optim( c(0,0), f )$par
  plot(cars)
  abline(model, col='red', lty=2)
  abline(opt[1], opt[2],col="blue")

library(quantreg)
plot(cars)
abline(model, col="blue")
abline(rq(dist ~ speed,data=cars, tau=.5),col="red",lty=2)
abline(rq(dist ~ speed,data=cars, tau=.9),col="purple",lty=2)

plot(model,which=1)

Scatterplot \((\widehat{Y}_i,\widehat{\varepsilon}_i)\)

plot(model,which=2)

Scatterplot \(\displaystyle{\left(\widehat{\varepsilon}_{i:n},\Phi^{-1} \left(\frac{i}{n}\right)\right)}\)

plot(model,which=3)

Scatterplot \((\widehat{Y}_i,\sqrt{\vert\widehat{\varepsilon}_i\vert})\)

plot(model,which=4)

Cook distance, \(\displaystyle{C_i=\frac{\widehat{\varepsilon}_i^2}{p\cdot\text{MSE}}\cdot\left(\frac{H_{i,i}}{(1-H_{i,i})^2}\right)}\) with \(\boldsymbol{H}=\boldsymbol{X}(\boldsymbol{X}^{\text{T}}\boldsymbol{X})^{-1}\boldsymbol{X}^{\text{T}}=[H_{i,i}]\)

C=cooks.distance(model)

\(H_{i,i}\) are leverages, and define Studentized residuals as \[ \widehat{r}_i=\frac{\widehat{\varepsilon}_i}{ \widehat{\sigma} \sqrt{1-H_{i,i}}} \]

rstudent(model)

##           1           2           3           4           5           6 
##  0.26345000  0.81607841 -0.39781154  0.81035256  0.14070334 -0.51716052 
##           7           8           9          10          11          12 
## -0.24624632  0.27983408  0.81090388 -0.57004675  0.15209173 -1.03037790 
##          13          14          15          16          17          18 
## -0.62992492 -0.36670509 -0.10509307 -0.49251696  0.02981715  0.02981715 
##          19          20          21          22          23          24 
##  0.81716230 -0.75078438 -0.09592079  1.49972043  3.02282876 -1.42097720 
##          25          26          27          28          29          30 
## -1.01227617  0.82440767 -0.87411459 -0.34752195 -1.13903469 -0.60553485 
##          31          32          33          34          35          36 
##  0.04737114 -0.73422040  0.18222855  1.52145888  2.09848208 -1.40929208 
##          37          38          39          40          41          42 
## -0.73145948  0.71330941 -1.98238877 -0.86293622 -0.59637646 -0.33247538 
##          43          44          45          46          47          48 
##  0.19208548 -0.19393283 -1.27493857 -0.45557342  1.02773460  1.09701943 
##          49          50 
##  3.18499284  0.28774529

plot(model,which=5)

Scatterplot \((H_{i,i},\widehat{r}_i)\)

plot(model,which=6)

Scatterplot \((H_{i,i},C_i)\)

hist(residuals(model),probability=TRUE, col="light green")
lines(density(residuals(model)),lwd=2,col="red")
boxplot(residuals(model),horizontal=TRUE,add=TRUE,at=.024, 
  pars=list(boxwex=.004),col=rgb(0,0,1,.25))

sigma=summary(model)$sigma
plot(ecdf(residuals(model)/sigma))
lines(seq(-3,3,by=.1),pnorm(seq(-3,3,by=.1)),lwd=2,col="red")

Kolmogorov-Smirnov $ d=\sup_{x\in\mathbb{R}}\lbrace \vert\Phi(x)-\widehat{F}_n(x)\vert \rbrace $

ks.test(residuals(model)/sigma,"pnorm")

## Warning in ks.test(residuals(model)/sigma, "pnorm"): ties should not be
## present for the Kolmogorov-Smirnov test

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  residuals(model)/sigma
## D = 0.13067, p-value = 0.3605
## alternative hypothesis: two-sided

Anderson-Darling, Cramer-von Mises,

library(nortest)
ad.test(residuals(model))

## 
##  Anderson-Darling normality test
## 
## data:  residuals(model)
## A = 0.79406, p-value = 0.0369

cvm.test(residuals(model))

## 
##  Cramer-von Mises normality test
## 
## data:  residuals(model)
## W = 0.12573, p-value = 0.0483

AIC \(AIC = 2k - 2\log(\mathcal{L}) = 2k + n\left[\log\left(2\pi \frac{1}{n}\sum_{i=1}^n \widehat{\varepsilon}_i^2 \right) + 1\right]\)

BIC \(BIC = { k \log(n) -2 \log(\mathcal{L}) } = k \log(n) + n\left[\log\left(2\pi \frac{1}{n}\sum_{i=1}^n \widehat{\varepsilon}_i^2 \right) + 1\right]\)

AIC(model)

## [1] 419.1569

AIC(model,k=log(n))

## [1] 424.8929

library(splines)
model_brk <- lm(dist ~ bs(speed,degree=1,knots=(c(4,15,25))), data=cars)
x=seq(4,25,by=.1)
y=predict(model_brk, newdata=data.frame(speed=x))

## Warning in predict.lm(model_brk, newdata = data.frame(speed = x)):
## prediction from a rank-deficient fit may be misleading

see \(b\)-splines, \[ y_i=\beta_0+\beta_1 x_i + \beta_2 (x_i-15)_+ + \varepsilon_i \]

plot(cars)
lines(x,y,lwd=2,col="blue")

positive=function(x,s) ifelse(x>s,x-s,0)
model_brk <- lm(dist ~ speed + positive(speed,15), data=cars)
x=seq(4,25,by=.1)
y=predict(model_brk, newdata=data.frame(speed=x))
plot(cars)
abline(model,col="red",lty=2)
lines(x,y,lwd=2,col="blue")

plot(cars)
abline(model,col="red",lty=2)
lines(x,y,lwd=2,col="blue")
abline(coefficients(model_brk)[1],coefficients(model_brk)[2],col="blue",lty=2)

summary(model_brk)$coefficients

##                      Estimate Std. Error    t value    Pr(>|t|)
## (Intercept)         -7.651916 10.6253642 -0.7201557 0.474995540
## speed                3.018648  0.8626766  3.4991649 0.001032415
## positive(speed, 15)  1.756247  1.4551278  1.2069365 0.233496132

library(strucchange)
plot(Fstats(dist ~ speed,data=cars,from=7/50))

see Chow Test

\[ W_t=\frac{1}{\widehat{\sigma}\sqrt{n}}\sum_{i=1}^{ \lfloor nt \rfloor} \widehat{\varepsilon}_i \]

cusum <- efp(dist ~ speed, type = "OLS-CUSUM",data=cars)
plot(cusum,ylim=c(-2,2))

plot(cusum, alpha = 0.05, alt.boundary = TRUE,ylim=c(-2,2))

see CUSUM test

model_cut=lm(dist~ cut(speed, breaks=c(0,10,15,20,25)),data=cars)
y=predict(model_cut, newdata=data.frame(speed=x))
plot(cars)
abline(model,col="red",lty=2)
lines(x,y,lwd=2,col="blue",type="s")

library(rpart)
tree=rpart(dist~speed,data=cars)
y=predict(tree,newdata=data.frame(speed=x))
plot(cars)
abline(model,col="red",lty=2)
lines(x,y,lwd=2,col="blue",type="s")

model_poly=lm(dist~ poly(speed, df=3),data=cars)
y=predict(model_poly, newdata=data.frame(speed=x))
plot(cars)
abline(model,col="red",lty=2)
lines(x,y,lwd=2,col="blue")

library(KernSmooth)
plot(cars)
bw <- dpill(cars$speed,cars$dist) 
lines( locpoly(cars$speed,cars$dist,degree=0, bandwidth=bw), col='red' )
lines( locpoly(cars$speed,cars$dist,degree=1, bandwidth=bw), col='green' )
lines( locpoly(cars$speed,cars$dist,degree=2, bandwidth=bw), col='blue' )

library(FNN)
knn=knn.reg(train=cars$speed,y=cars$dist,k=5)
plot(cars)
lines(cars$speed,knn$pred,col="red")

library(splines)
model_bs <- lm(dist ~ bs(speed), data=cars)
y=predict(model_bs, newdata=data.frame(speed=x))
plot(cars)
abline(model,col="red",lty=2)
lines(x,y,lwd=2,col="blue")

Tuning parameter selection, Silverman's Rule \[ b^\star=0.9 \cdot\frac{ \min\lbrace \sigma,F^{-1}(.75)-F^{-1}(.25)\rbrace}{1.34 \cdot n^{1/5}} \]

bw.nrd0(cars$speed)

## [1] 2.150016

See kernel regression

Tuning parameter selection, Cross Validation \[ b^\star=\text{argmin}\left\lbrace \sum_{i=1}^n \left(y_i - \widehat{m}_{(i)}(\boldsymbol{x}_i)\right)^2\right\rbrace \]

bw.ucv(cars$speed)

## Warning in bw.ucv(cars$speed): minimum occurred at one end of the range

## [1] 2.748934

library(KernSmooth)
Nadaraya_Watson =with(cars,ksmooth(speed, dist, "normal",bandwidth=2.75))
plot(cars)
abline(model,col="red",lty=2)
lines(Nadaraya_Watson,lwd=2,col="blue")

library(KernSmooth)
model_loess=loess(dist~ speed, data=cars,degree=1, family="gaussian")
y=predict(model_loess, newdata=data.frame(speed=x))
plot(cars)
abline(model,col="red",lty=2)
lines(x,y,lwd=2,col="blue")

Life Expectancy (1), Homicide Rate (2), Illiteracy Rate (3)

chicago=read.table("http://freakonometrics.free.fr/chicago.txt",header=TRUE,sep=";")
model_c = lm(Fire~X_2+X_3,data=chicago)
y=function(x2,x3) predict(model_c,newdata=data.frame(X_2=x2,X_3=x3))
VX2=seq(0,80,length=26); VX3=seq(5,25,length=26)
VY=outer(VX2,VX3,y)
persp(VX2,VX3,VY,xlab="Homicide",ylab="Illiteracy",zlab="Fire",theta=20)

VX2=seq(0,80,length=251); VX3=seq(5,25,length=251)
VY=outer(VX2,VX3,y)
image(VX2,VX3,VY,xlab="Homicide",ylab="Illiteracy")
contour(VX2,VX3,VY,add=TRUE)

model_c = lm(Fire~.,data=chicago)
summary(model_c)$r.squared

## [1] 0.4416723

summary(model_c)$adj.r.squared

## [1] 0.4027192

logLik(model_c)

## 'log Lik.' -152.7678 (df=5)

AIC(model_c, k=2)               # AIC

## [1] 315.5357

AIC(model_c, k=log(nrow(cars))) # BIC

## [1] 325.0958

\[ \widehat{\boldsymbol{\beta}} = \text{argmin}\left\lbrace \sum_{i=1}^n \left[y_i- \left(\beta_0+\sum_{j=1}^k \beta_j x_{j,i} \right)\right] + \color{red}{\lambda} \sum_{j=1}^k \vert \beta_j \vert\right\rbrace \] with an explicit solution \(\widehat{\boldsymbol{\beta}}=(\boldsymbol{X}^{\text{T}}\boldsymbol{X}-\color{red}{\lambda} \mathbb{I})^{-1} \boldsymbol{X}^{\text{T}}\boldsymbol{Y}\).

library(MASS)
model_ridge <- lm.ridge(Fire ~ ., data=chicago, lambda=1)

see more generally Tikhonov regularization

mse <- NULL
n=100
v <- matrix(c(0,coefficients(model_c)[-1]), nr=n, nc=4, byrow=TRUE)
kl <- c(1e-4, 2e-4, 5e-4, 1e-3, 2e-3, 5e-3, 1e-2, 2e-2, 5e-2, 
        .1, .2, .3, .4, .5, .6, .7, .8, .9, 1, 1.2, 1.4, 1.6, 1.8, 2)
for (k in kl) {
  r <- matrix(NA, nr=n, nc=4)
  for (i in 1:n) {
    boot_c <- chicago[sample(1:nrow(chicago),nrow(chicago),replace=TRUE),]
    r[i,2:4] <- model_ridge <- lm.ridge(Fire ~ ., data=boot_c, lambda=k)$coef
    r[i,1] <- mean(boot_c[,"Fire"])
  }
  mse <- append(mse, apply( (r-v)^2, 2, mean )[2])
}

plot( mse ~ kl, type='l' )  

step(lm(Fire ~ .,data=chicago))

## Start:  AIC=180.16
## Fire ~ X_1 + X_2 + X_3
## 
##        Df Sum of Sq    RSS    AIC
## - X_1   1      0.60 1832.4 178.17
## <none>              1831.8 180.16
## - X_2   1    561.94 2393.7 190.73
## - X_3   1    702.09 2533.8 193.41
## 
## Step:  AIC=178.17
## Fire ~ X_2 + X_3
## 
##        Df Sum of Sq    RSS    AIC
## <none>              1832.4 178.17
## - X_2   1    620.98 2453.3 189.89
## - X_3   1   1003.70 2836.1 196.70

## 
## Call:
## lm(formula = Fire ~ X_2 + X_3, data = chicago)
## 
## Coefficients:
## (Intercept)          X_2          X_3  
##     21.4965       0.2213      -1.5248

LASSO (least absolute shrinkage and selection operator) \[ \widehat{\boldsymbol{\beta}} = \text{argmin}\left\lbrace \sum_{i=1}^n \left[y_i- \left(\beta_0+\sum_{j=1}^k \beta_j x_{j,i} \right)\right] + \color{blue}{\lambda} \sum_{j=1}^k \beta_j^2\right\rbrace \]

library(glmnet)
fit = glmnet(x = as.matrix(chicago[,2:4]), y = chicago[,1], family = "gaussian", alpha = 1)
plot(fit, xvar="lambda", label = TRUE )

step(model)

## Start:  AIC=275.26
## dist ~ speed
## 
##         Df Sum of Sq   RSS    AIC
## <none>               11354 275.26
## - speed  1     21186 32539 325.91

## 
## Call:
## lm(formula = dist ~ speed, data = cars)
## 
## Coefficients:
## (Intercept)        speed  
##     -17.579        3.932

model_acp=lm(Fire ~ princomp(cbind(X_1,X_2,X_3))$scores[,1:3],data=chicago)
predict(model_c)[1:5]

##         1         2         3         4         5 
##  9.975499 16.985083 14.244580 13.411960 18.337225

predict(model_acp)[1:5]

##         1         2         3         4         5 
##  9.975499 16.985083 14.244580 13.411960 18.337225

model_acp=lm(Fire ~ princomp(cbind(X_1,X_2,X_3))$scores[,1:2],data=chicago)
predict(model_c)[1:5]

##         1         2         3         4         5 
##  9.975499 16.985083 14.244580 13.411960 18.337225

predict(model_acp)[1:5]

##        1        2        3        4        5 
## 10.01032 17.02103 14.29953 13.43876 18.39402

\[ \mathbb{E}[Y\vert \boldsymbol{X}=\boldsymbol{x}]= p(\boldsymbol{x})=\frac{\exp[\boldsymbol{x}^{\text{ T}}\boldsymbol{\beta}]}{1+\exp[\boldsymbol{x}^{\text{ T}}\boldsymbol{\beta}]}=H(\boldsymbol{x}^{\text{ T}}\boldsymbol{\beta}) \]

logistic regression

myocarde <-read.table("http://freakonometrics.free.fr/myocarde.csv", head=TRUE,sep=";")
model_bernoulli = glm(PRONO~., data=myocarde, family=binomial)
coefficients(summary(model_bernoulli))

##                  Estimate   Std. Error     z value  Pr(>|z|)
## (Intercept) -10.187641685 11.895227082 -0.85644785 0.3917501
## FRCAR         0.138178119  0.114112163  1.21089738 0.2259347
## INCAR        -5.862429035  6.748785486 -0.86866430 0.3850308
## INSYS         0.717084018  0.561444684  1.27721223 0.2015273
## PRDIA        -0.073668171  0.291636009 -0.25260314 0.8005749
## PAPUL         0.016756506  0.341942251  0.04900391 0.9609162
## PVENT        -0.106776012  0.110550096 -0.96586087 0.3341138
## REPUL        -0.003154187  0.004890917 -0.64490712 0.5189874

X=cbind(1,as.matrix(myocarde[,1:7]))
Y=myocarde$PRONO=="Survival"
beta=as.matrix(lm(Y~0+X)$coefficients,ncol=1)
for(s in 1:9){
   pi=exp(X%*%beta[,s])/(1+exp(X%*%beta[,s]))
   gradient=t(X)%*%(Y-pi)
   omega=matrix(0,nrow(X),nrow(X));diag(omega)=(pi*(1-pi))
   Hessian=-t(X)%*%omega%*%X
   beta=cbind(beta,beta[,s]-solve(Hessian)%*%gradient)}

 beta[,1]

##      X XFRCAR XINCAR XINSYS XPRDIA XPAPUL XPVENT XREPUL 
##      0      0      0      0      0      0      0      0

 beta[,9]

##             X        XFRCAR        XINCAR        XINSYS        XPRDIA 
## -9.202735e+00  4.772571e-14 -5.755396e-13  4.540812e-14  4.996004e-16 
##        XPAPUL        XPVENT        XREPUL 
##  2.664535e-15  1.387779e-15 -2.081668e-17

# -solve(Hessian)
sqrt(-diag(solve(Hessian)))

##                     FRCAR        INCAR        INSYS        PRDIA 
## 180.18368217   1.87748780  93.03024470   6.52098379   6.34628288 
##        PAPUL        PVENT        REPUL 
##   5.47188241   3.05900360   0.05472085

GLM <- glm(PRONO ~ PVENT + REPUL, data = myocarde, family = binomial)
pred_GLM = function(p,r){
 return(predict(GLM, newdata =
 data.frame(PVENT=p,REPUL=r), type="response"))}
vp=seq(min(myocarde$PVENT),max(myocarde$PVENT),length=251)
vr=seq(min(myocarde$REPUL),max(myocarde$REPUL),length=251)
vd=outer(vp,vr,pred_GLM)
library(RColorBrewer)
CL=colorRampPalette(brewer.pal(name="RdYlBu", 11))(100)

image(vp,vr,vd,col=CL,xlab="PVENT",ylab="REPUL")

probabilities <- predict(logistic, myocarde, type="response")

## Error in UseMethod("predict"): pas de méthode pour 'predict' applicable pour un objet de classe "function"

predictions <- levels(myocarde$PRONO)[(probabilities>.5)+1] 

## Error in eval(expr, envir, enclos): objet 'probabilities' introuvable

table(predictions, myocarde$PRONO)

## Error in table(predictions, myocarde$PRONO): objet 'predictions' introuvable

Pearson's residuals \[ \widehat{\varepsilon}_i=\frac{y_i - \widehat{\pi}_i}{ \sqrt{\widehat{\pi}_i\cdot[1-\widehat{\pi}_i]}} \] Deviance residuals \[ \widehat{\varepsilon}_i=\pm \left( y_i \log[\widehat{\pi}_i]+ (1-y_i) \log[1-\widehat{\pi}_i]\right) \]

E1=residuals(model_bernoulli,type="pearson")
E2=residuals(model_bernoulli,type="deviance")

plot(1:nrow(myocarde),E1)

Binomial case, \(Y\in\lbrace 0,1\rbrace\),

\(\mathbb{P}[Y=1\vert \boldsymbol{X}=\boldsymbol{x}]\propto\exp[\boldsymbol{x}^{\text{ T}}\boldsymbol{\beta}]\)

\(\mathbb{P}[Y=0\vert \boldsymbol{X}=\boldsymbol{x}]\propto1\)

Multinomial case, \(Y\in\lbrace A,B,C\rbrace\),

\(\mathbb{P}[Y=\color{red}{A}\vert \boldsymbol{X}=\boldsymbol{x}]\propto\exp[\boldsymbol{x}^{\text{ T}}\color{red}{\boldsymbol{\beta}_A}]\)

\(\mathbb{P}[Y=\color{blue}{B}\vert \boldsymbol{X}=\boldsymbol{x}]\propto\exp[\boldsymbol{x}^{\text{ T}}\color{blue}{\boldsymbol{\beta}_B}]\)

\(\mathbb{P}[Y=\color{green}{C}\vert \boldsymbol{X}=\boldsymbol{x}]\propto1\)

library(VGAM)
model_multi = vglm(PRONO~., data=myocarde, family="multinomial")
model_multi

## Call:
## vglm(formula = PRONO ~ ., family = "multinomial", data = myocarde)
## 
## Coefficients:
##  (Intercept)        FRCAR        INCAR        INSYS        PRDIA 
## 10.187641072 -0.138178115  5.862428927 -0.717083993  0.073668174 
##        PAPUL        PVENT        REPUL 
## -0.016756516  0.106776011  0.003154187 
## 
## Degrees of Freedom: 71 Total; 63 Residual
## Residual deviance: 41.04314 
## Log-likelihood: -20.52157

Poisson and Gamma distributions in the exponential family

base=data.frame(x=c(1,2,3,4,5),y=c(1,2,4,2,6))
regNId <- glm(y~x,family=gaussian(link="identity"),data=base)
regNlog <- glm(y~x,family=gaussian(link="log"),data=base)
regPId <- glm(y~x,family=poisson(link="identity"),data=base)
regPlog <- glm(y~x,family=poisson(link="log"),data=base)
regGId <- glm(y~x,family=Gamma(link="identity"),data=base)
regGlog <- glm(y~x,family=Gamma(link="log"),data=base)

visuel=function(regression,titre=""){
 plot(base$x,base$y,pch=19,cex=1.5,main=titre,xlab="",ylab="")
 abs <- seq(0,7,by=.1)
 yp <- predict(regression,newdata=data.frame(x=abs),se.fit = TRUE, type="response")
 polygon(c(abs,rev(abs)),c(yp$fit+2*yp$se.fit,rev(yp$fit-2*yp$se.fit)), col="light green",border=NA)
 points(base$x,base$y,pch=19,cex=1.5)
 lines(abs,yp$fit,lwd=2,col="red")
 lines(abs,yp$fit+2*yp$se.fit,lty=2)
 lines(abs,yp$fit-2*yp$se.fit,lty=2)}

visuel(regNId,"Gaussienne, lien identité")

visuel(regPId,"Poisson, lien identité")

visuel(regGId,"Gamma, lien identité")

visuel(regNlog,"Gaussienne, lien logarithmique")

visuel(regPlog,"Poisson, lien logarithme")

visuel(regGlog,"Gamma, lien logarithme")